La multitud de Deulofeu.
Ciclos generacionales. Sábado, 13 de Julio de 2019.
La Historia se repite pero ¿cada cuánto?
Cliodinámica. Matemáticas. Teoría cíclica.
La multitud de Deulofeu.
E pluribus unum.
El maestro Deulofeu tuvo la visión de las sociedades como si fueran un organismo vivo, compuesto de sus múltiples órganos. Y acertó, concentrándose en la evidencia de que todo ser vivo atraviesa un ciclo de vida y muerte; sin embargo, esa imagen lleva tal vez a equívocos si no ampliamos el concepto.
Un cuerpo humano o un organismo es en el fondo la asociación de una multitud de células funcionales y especializadas que interactúan de modo muy complejo, formando por ello un sistema dinámico.
Pero hay muchos posibles. Por ejemplo, los ecosistemas que degradan las aguas residuales.
En función de las condiciones ambientales y los microorganismos presentes, se forman auténticos muestrarios biológicos de alta diversidad, que se expanden a expensas de la materia orgánica; después continúan hasta devorarla por completo y finalmente se devoran a sí mismos.
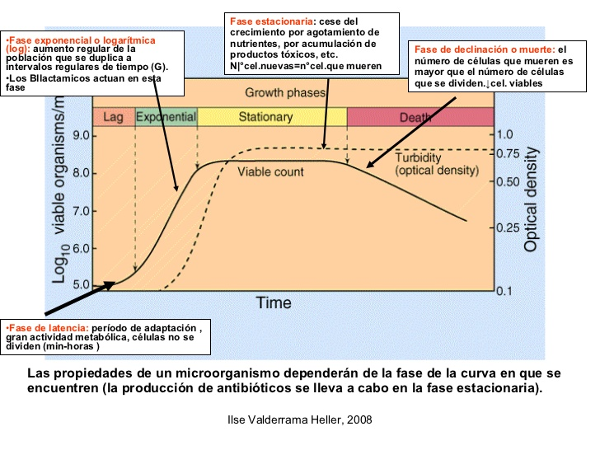
Esto se puede observar en un típico gráfico de evolución de la población bacteriana en un cultivo. En biología y en ingeniería ambiental, es conocida la siguiente gráfica:
El ramal ascendente de la curva se puede modelizar matemáticamente con las ecuaciones:
De hecho, en un ecosistema cerrado la curva es doble. Cuando parece que todo va a terminar, el sistema se recupera fagocitando los cadáveres de los microorganismos que perecen. Eso hace que se recupere la población y vuelva a crecer, al menos hasta que esa población vuelve a degradarse y decae nuevamente, desapareciendo finalmente.
Por cierto, que las distintas especies que forman el cultivo no se convierten en una especie nueva y homogénea durante el tiempo que dura la vida colectiva, pasando a ser grupos distintos al terminar ese tiempo. Aunque, ciertamente, siempre hay alguna cepa que se impone a las demás y reprime su crecimiento.
Casualmente, un imperio viene a ser algo parecido, un conjunto heterogéneo de organismos (pueblos) creciendo y expandiéndose a costa de un sustrato de recursos.
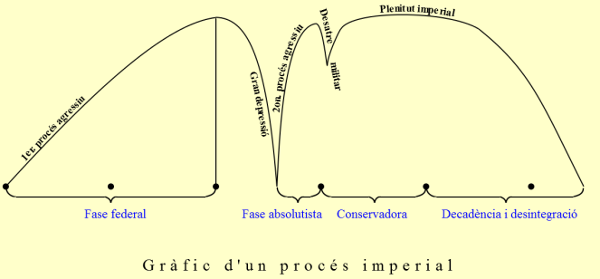
Deulofeu nos explica el proceso imperial en «Naixement, grandesa i mort de les civilitzacions» («Nacimiento, grandeza y muerte de les civilizaciones»):
Tenemos que tener en cuenta que ahora no se trata de un ciclo evolutivo, sino de un proceso biológico…
…La gráfica del proceso imperial… sigue una línea contínuamente ascendiente. Llegamos a un momento,… sigue un camino descendente… todo nos dirige a creer que ha muerto.
La facción triunfante,… recupera los territorios perdidos.
Llegamos a la plenitud imperial… la representamos en un trazo horizontal…
Llegando a la fase decandente es cuando la gráfica empieza a bajar… hasta llegar a la desaparición total del Imperio bajo dominio de otro núcleo imperial o por la llegada de la época de gran fraccionamiento demográfico.
Gráficamente:
A propósito de Malthus.
Malthus afirmaba que el crecimiento de la población es exponencial (progresión geométrica), mientras que el crecimiento de los recursos es lineal (progresión aritmética). Si la población crece más deprisa que los recursos, se produce una catástrofe y debe regularse la natalidad para que «desaparezcan» aquellos que «sobran». Genial, si no es usted el que se ha de sacrificar ¿verdad?
Su deducción se describe justamente en la ecuación que hemos visto antes: (dN/dt) = kN, donde N es la población. Aquí «k» es una constante, un número; sin embargo, podemos sustituir esa «k» por una función del tiempo que involucre más variables, por lo que la curva explosiva de crecimiento no es indefinida.
Deulofeu nos ha dado una función descriptiva de las variantes a esa curva. También nos ha dado otra respuesta a la cuestión planteada por Malthus: la Naturaleza evita la destrucción dándonos tiempo limitado para realizarla.
Además, hay otros indicios que nos dicen cómo resolvieron estas contingencias en el pasado. Quizás en los números hallemos una aportación a la arqueología de las civilizaciones.
Salud y hasta pronto.
Enlace del artículo original:
https://timecycleblog.wordpress.com/2019/07/13/la-multitud-de-deulofeu-deulofeus-plenty/